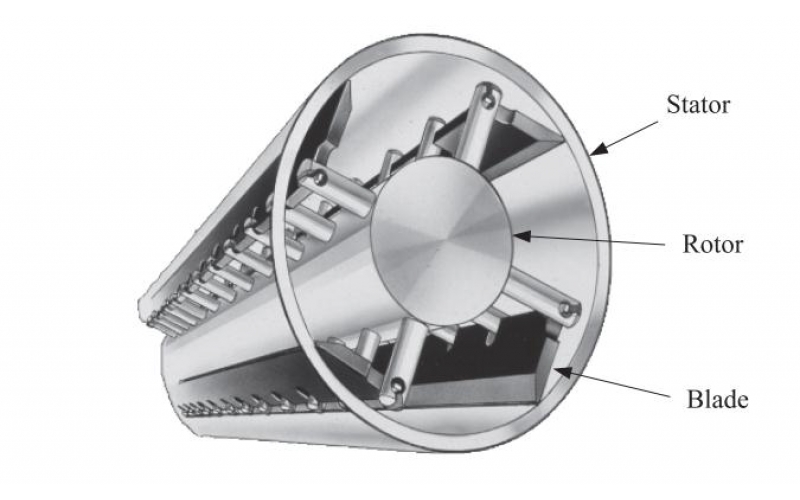
En enkel matematisk modell av væskestrømning i en vanlig type varmeveksler med skrapet overflate hvor gapene mellom bladene og apparatveggene er smale, slik at en smøre-teoretisk beskrivelse av strømmen er gyldig, presenteres. Spesifikt er jevn isoterm strømning av en newtonsk væske rundt en periodisk rekke dreide skrapeblader i en kanal med en stasjonær og en bevegelig vegg, når det er en påført trykkgradient i en retning vinkelrett på veggbevegelsen, analyse. Strømmen er tredimensjonal, men dekomponerer naturlig til en todimensjonal "tverrgående" strømning drevet av grensebevegelsen og en "langsgående" trykkdrevet strømning. De første detaljer om strukturen til tverrstrømmen utledes, og spesielt likevektsposisjonene til bladene beregnes. Det er vist at den ønskede kontakten mellom bladene og den bevegelige veggen vil bli oppnådd, forutsatt at bladene svinges tilstrekkelig tett inntil endene. Når den ønskede kontakten er oppnådd, forutsier modellen at kreftene og dreiemomentene på bladene er enkeltstående, og derfor generaliseres modellen til å inkludere ytterligere tre fysiske effekter, nemlig ikke-newtonsk kraftlovadferd, glidning ved stive grenser og kavitasjon i områder med svært lavt trykk, som hver viser seg å løse disse singularitetene. Til slutt diskuteres arten av den langsgående strømmen.